

Note : je serais très heureux de recevoir des suggestions ou des remarques en vue de l'amélioration des ouvrages mentionnés dans ce site - ou pour l'amélioration de ce site même.
Si vous rencontrez des difficultés avec l'un des exercices ou problèmes de l'un de mes livres, ou avec une question d'examen, envoyez-moi un message, avec une description aussi précise que possible de vos difficultés et de votre approche du problème. J'essaierai d'y répondre rapidement. Désolé ! pas de courrier snail-mail (papier, enveloppe, timbre, boîte aux lettres, poste, etc.).
Les questions les plus intéressantes (avec leur réponses) sont regroupées (anonymement) ci-dessous :
Question : La formule donnée à la section 12.1.8 du livre « Le Radio-Amateur, 2e édition » ou section 11.1.8 du livre « Le Radio-Amateur, 3e édition » ou section 12.1.8 du livre « Le Radioamateur, 4e édition » pour le calcul du rapport de transformation d'un transformateur donne les bons résultats dans le cas d'un transformateur abaisseur, mais ne semble pas s'appliquer au cas d'un transformateur élévateur. Qu'en est-il ? (Note : cette section a été améliorée pour les 3e et 4e éditions).
En effet cette formule permet de calculer directement le rapport de transformation dans le cas d'un transformateur abaisseur, par exemple pour un transformateur de primaire 230 V et se secondaire 23 V, elle donne un rapport de transformation de 10.
Normalement un tel rapport s'exprime 10:1 pour bien exprimer l'effet abaisseur (ici de tension) du transformateur.
Si le même transformateur est utilisé dans l'autre sens, en élévateur, c'est-à-dire avec une tension primaire de 23 V et une tension secondaire de 230 V, l'application de la formule donne un rapport de 0,1.
Selon la remarque ci-dessus, ce rapport est en fait 0,1:1 ce qui en représentation plus conventionnelle pour une fraction donne :
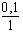
La même fraction multipliée au numérateur et au dénominateur par 10 ne change pas de valeur et devient :
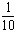
A ce stade, il y a 2 options pour le lecteur confronté à la question posée :
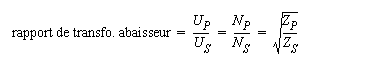
Si l'on a affaire à un transformateur élévateur, on se sert de l'inverse de la formule ci-dessus, soit :
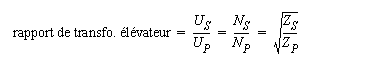
Note : même dans ce cas il convient de faire attention en interprétant le format du résultat : soit x:1 pour un transformateur abaisseur et 1:x pour un transformateur élévateur.
 Comment déterminer le type d'un filtre
Comment déterminer le type d'un filtre
Question : Comment déterminer si un circuit RL, RC ou RLC est un filtre passe-haut ou passe-bas ?
Il suffit de considérer ce qui se passe pour des fréquences extrêmement élevées ou au contraire extrêmement basses.
Une fréquence extrêmement élevée est difficile à conceptualiser, mais une fréquence extrêmement basse est tout-à-fait dans nos cordes, puisque le courant continu peut effectivement être considéré comme la fréquence la plus basse qui soit.
En effet une fréquence basse ne varie pas un grand nombre de fois par secondes, et une fréquence extrêmement basse varie si peu souvent qu'elle ne varie quasiment pas du tout, comme par exemple une tension continue. Le truc est donc d'analyser le circuit en examinant son comportement en présence d'une tension continue. si cette dernière est transmise, on est en présence d'un circuit passe-bas, dans le cas contraire, on a affaire à un filtre passe-haut.
Maintenant, il devient aisé d'analyser le fonctionnement de tout filtre passif simple, puisque l'on sait qu'un condensateur ne laisse pas passer une composante continue, alors qu'une self n'oppose aucune impédance au passage de cette dernière.
Voici à titre d'exemple deux filtres, et le raisonnement nécessaire à leur analyse.
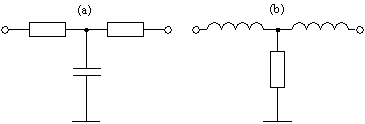
Dans le circuit (a), les résistances n'ont pas un comportement qui varie en fonction de la fréquence, cependant le condensateur n'a aucune influence en courant continu, c'est-à-dire pour les très basses fréquences. Il semble que ce circuit soit donc un filtre passe-bas puisque le courant continu n'y est pas affecté. D'un autre coté, nous savons que ce même condensateur est un court-circuit pour les fréquences très élevées, et qu'il les court-circuitent donc vers la masse. Ces fréquences ne se retrouvent ainsi pas à la sortie, ce qui confirme que ce circuit est bien un filtre passe-bas.
En (b), les inductances n'ont aucune influence en courant continu (elles ne présentent aucune impédance) quant à la résistance, sont comportement ne varie pas en fonction de la fréquence. Puisque les inductances laissent passer les très basses fréquences sans encombre, nous sommes en présence d'un circuit passe-bas. A titre de confirmation, nous pouvons considérer que les inductances présentent une impédance élevée aux fréquences hautes, ce qui contribue à les éliminer de la sortie du filtre.
 Mise en série de condensateurs
Mise en série de condensateurs
Question : Pourquoi mettre une résistance en parallèle sur des condensateurs en série, comme indiqué à la réponse R2.17 (4e édition) ou R2.20 (5e édition du livre « Le Radio-Amateur » ?
Généralement, la mise en série de composants identiques a pour but de réaliser des circuits pouvant supporter une tension supérieure à celle possible avec un simple élément.
Deux cas sont intéressants, soit celui de la mise en série de condensateurs, comme mentionné dans l'énoncé de cette question, soit la mise en série de diodes, par exemple dans un pont redresseur. Nous allons parler de ce dernier cas dans la seconde partie de cette réponse. Commençons par étudier la mise en série de condensateurs.
Admettons que nous désirions placer un condensateur aux bornes d'un circuit où se trouve une tension supérieure à celle que peut supporter le condensateur dont nous disposons. Considérons par exemple que la tension dans le circuit est de 150 V et que notre condensateur ne peut supporter plus de 100 V. Nous pouvons bien entendu nous procurer un autre condensateur à même de supporter les 150 V de notre circuit, mais nous pouvons aussi placer deux condensateurs en série, pour une tension maximale supportable de 200 V.
La mise en série de deux condensateurs en série, suppose que la tension va se répartir également entre eux, soit ici, 75 V par élément. Mais qu'est-ce qui va garantir cette répartition ?.
Oublions tout de suite tout ce que nous pouvons envisager d'idéal, les effets en jeu ici sont en rapport avec la « non-idéalité » des composants. En effet, le diélectrique de nos condensateurs, particulièrement si ceux-ci sont de forte valeur, présente une certaine résistance de fuite (aucun isolant n'est parfait).
Chacun de nos condensateur peut donc être assimilé à un condensateur parfait en parallèle avec une résistance de très forte valeur représentant le courant de fuite du diélectrique.
A titre d'exemple, voici ce que l'on peut trouver dans un catalogue récent de condensateurs : Ifuite = 2.10-8 x C x V ce qui pour un condensateur de 220 uF chargé à 75 V nous donne : Ifuite = 330 pA. Cependant le fabricant précise que ce courant peut atteindre 3 uA au maximum. Cette variation est très importante et meme peu réaliste. Cependant elle nous indique que 2 de ces condensateurs, l'un très bon du point de vue courant de fuite et l'autre passablement moins bon produiront le circuit suivant (a) s'il sont montés en serie.
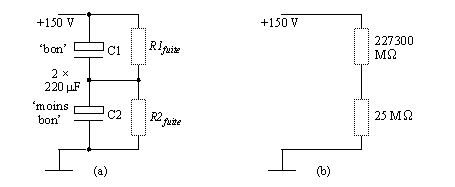
Notons que 330 pA sous 75 V correspondent à une résistance de fuite de 227.3 Gohms (227300 Mohms) alors que 3 uA correspondent à une résistance de fuite de 25 Mohms.
Ici les condensateurs sont donc des éléments idéaux, en parallèle avec une résistance représentant leur courant de fuite. La tension aux bornes de ces deux condensateurs va donc se répartir en proportion de leurs résistances de fuite, cela peut aisément se calculer au moyen de la Loi d'Ohm. (fig. b ci-dessus).
Ici, pour une tension totale de 150 V, nous aurons 16 mV aux bornes du « mauvais » condensateur et 149.984 V aux bornes du meilleur. Puisque ces éléments ne sont pas censés supporter plus de 100 V chacun, il est probable que le « bon » condensateur va être détruit par cette surtension a ses bornes.
S'il se met en court-circuit, ce qui est vraisemblable, la totalité de la tension va alors se retrouver aux bornes du second condensateur qui va lui-même se détruire.
Une autre façon d'appréhender la répartition de la tension totale entre les deux condensateurs, est de considérer que puisqu'ils sont en série, et que le courant (de fuite) qui nous intéresse doit être identique entre les deux résistances, il faut que les tensions se répartissent en conséquence (fig. b ci-dessus).
La solution est donc d'aider la tension à se répartir entre les deux condensateurs en ajoutant des résistances en parallèle sur les condensateurs de façon à égaliser leurs courants de fuite apparents.
Analysons le circuit ci-dessous, dans lequel nous avons placé des résistances de 4,7 Mohms en parallèle sur chaque condensateur.
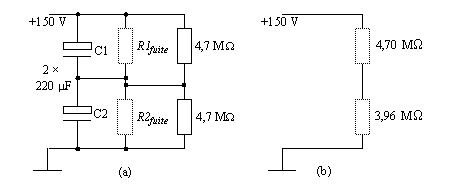
Le « bon » condensateur voit une résistance totale de 4,7 Mohms en parallèle avec une résistance de 227300 Mohms, soit quasiment 4,7 Mohms. L'autre condensateur voit une résistance équivalente de 4,7 Mohms en parallèle avec 25 Mohms, soit 3,96 Mohms (fig. b ci-dessus).
La tension va ainsi se répartir en proportion de ces nouvelles valeurs, et nous trouvons maintenant 81,4 V aux bornes du meilleur élément et 68,6 V aux bornes de l'autre. Non seulement une bien meilleure situation, mais une situation parfaitement acceptable puisqu'aucun des 2 condensateurs ne voit une tension supérieure aux 100 V qu'il peut supporter au maximum.
Note : pour effectuer les calculs ci-dessus, on peut faire abstraction des condensateurs, puisque l'on se trouve en courant continu, et les différents cas se réduisent a de simples problèmes de sources de tension et de résistances.
Note : bien entendu, si l'on place deux condensateurs en série, la valeur de capacité résultante et divisée par deux. Il faut dans ce cas monter 4 éléments en série/paralléle comme indiqué dans la réponse de l'exercice R2.17 (4e édition) ou R2.20 (5e édition).
Un autre cas est intéressant, c'est celui de la mise en série de diodes pour
redresser des tensions élevées.
Dans ce cas, on ne s'intéresse pas à la tension des diodes quand elles conduisent puisque cette tension est faible, mais lorsqu'elles sont polarisées en inverse et qu'elles ne conduisent pas. Il faut à ce moment-là s'assurer que la tension se répartisse également entre les différentes diodes. Ici encore, il s'agit d'égaliser le courant inverse de fuite des diodes.
Puisque nous sommes en alternatif, l'élément à même d'effectuer cette tâche est un petit condensateur, de faible valeur. Le schéma suivant en montre le principe.
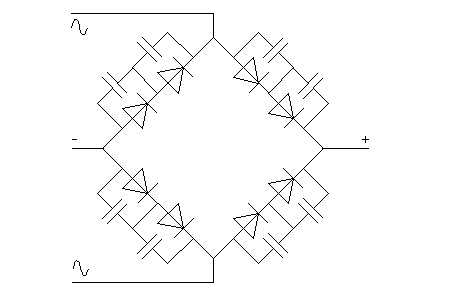
Dans les grandes lignes, les calculs sont les mêmes que ci-dessus et ne sont pas répétés ici. Il faut ainsi partir d'une estimation des extrêmes du courant inverse de fuite des diodes. On détermine alors quelle valeur de condensateur va laisser passer un courant (alternatif) suffisamment important (par exemple 5 fois plus important que le courant de fuite le plus élevé prévu), pour égaliser la tension entre les diodes.
Note : le lecteur peut penser à ce point que la mise en parallèle de condensateurs sur les diodes ou de résistances sur des condensateurs nuit à la qualité du circuit, en introduisant des fuites ou des pertes supplémentaires. En réalité, les non-idéalités ainsi introduites sont si faibles qu'elles sont imperceptibles et sans conséquence, seul subsiste l'effet positif de cette technique.
 Aspect « résistif » d'une antenne.
Aspect « résistif » d'une antenne.
Question : Il me semble qu'un dipôle devrait se comporter comme un circuit ouvert et un dipôle replié comme un court-circuit, pourtant il semble que ce ne soit pas le cas. Qu'en est-il ?
Comme toutes les questions simples, celle-ci a plusieurs réponses, dont les plus satisfaisantes sont les plus complexes. Essayons cependant d'apréhender la solution au travers des aspects simples de ce sujet.
a) Il n'y a de puissance qu'en présence d'une résistance (voir aussi sur ce site le tutorial sur la puissance, entre autres la section 4.2 : Tutorial sur la puissance).
b) Une antenne, quel que soit sont type, émet de la puissance sous forme d'un rayonnement électromagnétique. Pour l'émetteur alimentant cette antenne, tout se passe comme s'il était en présence d'une résistance absorbant une puissance équivalente à celle rayonnée par l'antenne. La puissance émise par l'antenne semble ainsi dissipée par l'antenne telle la puissance dissipée par une résistance. Cette résistance équivalente est appelée résistance de rayonnement et vaut de l'ordre de 73 ohms dans un dipôle ouvert, 300 ohms dans un dipôle replié et 37 ohms dans le cas d'un quart d'onde.
c) Une antenne est assimilable à un circuit LC. Or nous savons qu'en haute fréquence, un simple conducteur ne se comporte plus comme un simple conducteur. Sont inductance propre devient non-négligeable, et sa capacité, avec lui-même, d'autres conducteurs plus ou moins proches ou simplement toute masse environnante (y compris la terre), doit aussi être prise en compte.
Bien entendu, ceci nous fournit un circuit LC, et explique q'une antenne présente une impédance soit capacitive, soit inductive pour les fréquences de part et d'autre de sa fréquence de résonance. Finalement, puisqu'une puissance est émise, soit perdue (du point de vue du circuit oscillant équivalent à notre antenne), notre modèle doit comporter une résistance.
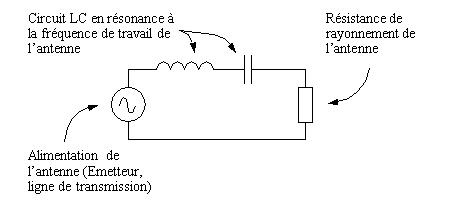
La figure ci-dessus représente le circuit électrique équivalent à une antenne, soit le modèle de l'antenne. Un tel circuit peut être utilisé lors de la conception d'un appareil émetteur pour modéliser l'antenne lors des simulations électroniques (Voir Simulation électronique).
Il faut noter que dans un tel modèle, qui cherche à représenter électriquement le comportement de l'antenne, il n'y a pas nécessairement de correspondance directe entre les éléments du modèle et la réalité. Ici, l'inductance existe de par les conducteurs constituant l'antenne. La capacité existe aussi entre les différentes masses constituant l'antenne et son environnement. La résistance n'existe pas réellement, mais vise à reproduire le comportement de l'antenne, qui semble absorber la puissance fournie par l'émetteur.
Note : en réalité, la résistance « visible » aux bornes de l'antenne comporte en plus de la résistance de rayonnement une seconde composante due aux pertes (résistance des conducteurs, pertes dans les isolants, etc.). Dans certains type d'antenne, cette seconde composante peut être relativement importante, et devrait être minimisée, car elle représente une puissance perdue, c'est-à-dire non émise.
Question : Comment se fait-il qu'un segment de ligne de transmission effectue une transformation d'impédance ou fasse fonction de balun ?
Commençons par étudier le comportement de segments de ligne, puis dans la seconde partie de cette réponse, nous parlerons des baluns.
La loi d'Ohm nous enseigne que le courant, la tension et la résistance sont indissociables. En HF, on parle plus volontier d'impédance, mais on s'intéresse le plus souvent à la partie réelle de cette impédance, soit la partie résistive.
Ainsi, une ligne de transmission proprement terminée, présente à son autre extrémité un « reflet » de cette terminaison (voir figure ci-dessous).

De même, un segment de ligne improprement ou non terminé, présente à son entrée un « reflet » de cette terminaison impropre, mais ce reflet subit alors une transformation, le long du segment de ligne, qui dépend de la longueur de la ligne.
Par longueur de ligne, il faut bien entendu comprendre « longueur électrique de la ligne », qui est plus longue que la longueur physique de cette ligne en fonction du facteur de vélocité. Ceci est expliqué en détail dans le livre Le Radioamateur, 2e édition, section 24.2.2, 3e édition, section 24.2.3, 4e édition, section 24.2.3.
Considérons d'abord 2 segments de 1/4 de longueur d'onde, l'un terminé par un court-circuit (a) et l'autre (b) non-terminé (ouvert). Voyons la répartition du courant et de la tension le long de ce segment.
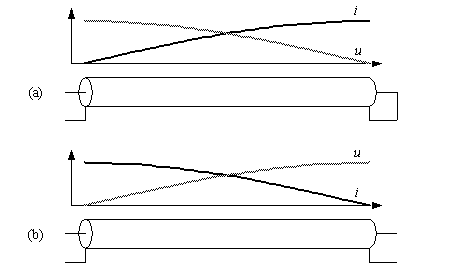
En (a), puisque le segment se termine par un court-circuit, il ne peut y avoir de tension dans ce court-circuit. La tension en ce point est 0 V. Ceci « fixe » une référence pour la distribution de la tension le long de la ligne. Quant au courant, il ne peut être que maximum dans un court-circuit. Ceci fixe aussi une référence pour la distribution du courant le long de la ligne. Une autre façon d'apréhender la distribution du courant, est de considérer que puisqu'il n'y a pas de résistance (dans le court-circuit), le courant doit être déphasé de 90 degrés, et doit donc être maximal quand la tension est nulle. En (b), puisque le segment est ouvert, il ne peut y avoir de courant en ce point, par contre la tension est bien maximale. Ceci fixe dans ce cas un point de référence pour le courant et la tension le long de ce segment de ligne.
Maintenant que nous avons fixé la distribution du courant et de la tension le long de la ligne, nous pouvons examiner ce qu'il se passe à l'autre extrémité de la ligne, du coté de l'entrée.
Si l'on se réfère à la figure (a) ci-dessus, on remarque qu'à l'entrée, le courant est nul et la tension maximale. Que dire d'une structure qui n'est pas le siège d'un courant quand on lui applique une tension ? que c'est un isolant, bien sûr. Cependant, cet isolant présente deux particularités, il n'est pas isolant en courant continu, et il n'est isolant qu'à la fréquence pour laquelle il représente 1/4 de longueur d'onde (ou aux fréquences pour lesquelles il présente un nombre impair de 1/4 de longueur d'onde).
Dans le cas de la figure (b), la situation est inversée et l'entrée de notre segment représente un court-circuit pour une fréquence (ou aux fréquences pour lesquelles il présente un nombre impair de 1/4 de longueur d'onde), sans toutefois présenter de court-circuit pour le courant continu.
Seule l'imagination limite les possibilités d'utilisation de ces 2 éléments, citons par exemple dans le cas du 1/4 d'onde fermé, la possibilité de réaliser des supports pour des lignes de puissance (figure (a) ci-dessous), et dans le cas du 1/4 d'onde ouvert, la réalisation beaucoup plus commune de filtres notch ou trappes (figure (b) ci-dessous).
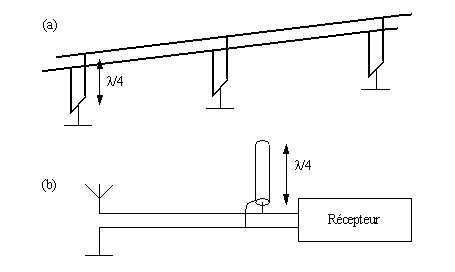
Ici à la figure (a), la ligne de transmission est mise à la masse (du point de vue du courant continu, mais est parfaitement isolée à la fréquence pour laquelle les 1/4 d'onde ont été conçus. En (b), un signal perturbateur est efficacement éliminé par un 1/4 d'onde ouvert placé à l'entrée du récepteur.
D'autres configurations sont possibles, voyons par exemple le comportement d'un segment de 1/2 longueur d'onde. La figure suivante illustre ce cas. Puisqu'une ligne de 1/2 de longueur d'onde correspond à 2 x 1/4 de longueur d'onde, on peut s'attendre à retrouver ce comportement
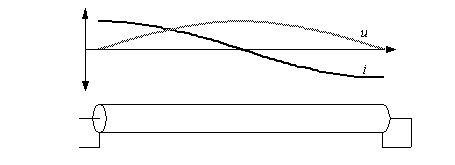
Considérons par exemple un segment de ligne en court-circuit. La tension est donc nulle en fin de ligne (dans le court-circuit), alors que le courant y est maximal (ici négatif). Nous constatons alors que la tension et le courant sont identiques à l'autre extrémité de la ligne, excepté que le courant y est inversé. Ceci implique que l'impédance en fin de ligne est « miroitée » à l'autre extrémité de la ligne, mais avec un déphasage de 180 degrés. En fait, quelle que soit sa terminaison, un segment de ligne de 1/2 de longueur d'onde, présente une « copie » de son impédance de terminaison sur son entrée, avec un déphasage de 180 degrés.
Voici une application de cet élément, sous forme d'un balun 4:1 pour alimenter une antenne symétrique de 200 ohms à partir d'une ligne asymétrique de 50 ohms.
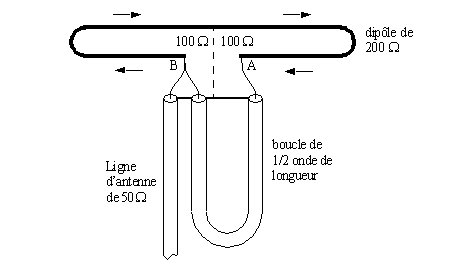
On reconnait un dipôle fermé, nécessitant une alimentation symétrique. Il est alimenté ici par une ligne asymétrique (coaxiale) de 50 ohms. La boucle de 1/2 longueur d'onde sert de transformateur d'impédance dans un rapport de 4:1. Notre dipôle (structure symétrique) étant de 200 ohms d'impédance, est constitué de deux demi-structures de 100 ohms en série. Entre les points A et B, il y a 200 ohms, mais entre chacun des point A, B et la masse, il y a 100 ohms. La masse, se trouve représentée d'une part par le blindage des lignes coaxiales, et d'autre part par le point central du dipôle; d'ailleurs ces deux points peuvent (et même devraient) être reliés (ligne pointillée).
Considérons d'abord le point A, qui présente une impédance de 100 ohms par rapport à la masse. Cette impédance est « miroitée » à l'autre extrémité du segment de 1/2 onde. Entre le point B et la masse, l'impédance est aussi de 100 ohms. Ainsi la connexion en parallèle des 100 ohms du demi-dipôle B et des 100 ohms « réfléchis » par le segment de ligne donne 50 ohms, qui sont alimentés par la ligne d'antenne de 50 ohms.
On remarque aussi les petites flèches le long du dipôle, qui représentent le courant à un instant donné. Le courant sort de B et rentre en A, ce qui correspond à un déphasage de 180 degrés, exactement ce que notre segment de 1/2 longueur d'onde peut fournir.
Voilà donc le principe de fonctionnement de ce montage balun, transformateur d'impédance. Bien entendu, ce montage est aussi valable si le dipôle présente une impédance de 300 ohms, et que les lignes sont de 75 ohms. Dans la pratique, il est aussi possible que le dipôle fasse 300 ohms et que la ligne soit de 50 ohms; dans ce cas, l'adaptation n'est pas parfaite, mais généralement suffisante.
Il existe de nombreuses autres applications des segments de ligne, souvent mieux expliqués par l'utilisation de l'abaque de Smith (Smith chart) avec laquelle il est utile de se familiariser si l'on veut poursuivre plus avant des investigations dans le domaine des adaptations d'impédance en haute fréquence. Enfin, les ouvrages sur les antennes destinés aux radioamateurs donnes de nombreux exemples pratiques de ces circuits pour l'alimentation d'antennes et les adaptations d'impédances.
Question : J'ai un doute concernant la notion de TOS. Le TOS est quelquefois nommé ROS, alors que le TOS est 100 x le coefficient de réflexion. Pouvez-vous préciser cette notion ?
D'abord un petit rappel sur les notions de ROS et coefficient de réflexion ne peut
nuire à personne.
Le coefficient de réflexion, communément représenté par la lettre Grecque gamma majuscule ( )
et le ROS (ou SWR en anglais) sont donnés par les expressions suivantes :
)
et le ROS (ou SWR en anglais) sont donnés par les expressions suivantes :
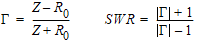
Bien que travaillant dans le domaine de la haute fréquence depuis bien des années et étant radioamateur depuis pas mal de temps, je n'ai jamais rencontré la notion de TOS mentionnée dans la question. Une petite recherche sur le web m'a cependant permis de vérifier que quelques auteurs, tous Francais, font utilisation de ce terme, en précisant toutefois qu'il est désuet.
Quelques amateurs utilisent TOS et ROS pour parler de la même chose, c'est-à-dire le ROS (ce que les anglais - qui ignorent la notion de TOS - appellent SWR ou VSWR).
La notion de TOS telle que mentionnée dans la question n'est qu'une variation du coefficient de réflexion, qui serait plus aptement dénommée « pourcentage de réflexion ». En fait, pour être rigoureux, il ne faudrait utiliser que le terme de ROS (Rapport d'Ondes Stationnaires), le TOS, étant un Taux, ne devant aller que de 0 à 1 (ou de 0 à 100%). Donc puisque le TOS fait double emploi avec le coefficient de réflexion et que c'est une notion surranée, je propose de ne plus l'utiliser.
En conclusion, la pratique veut que l'on parle de coefficient de réflexion
( ), et que l'on ne considère que le ROS :
), et que l'on ne considère que le ROS :
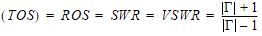
Dans le même ordre d'idée, les anglo-saxons utilisent unanimement le SWR ou VSWR, notions identiques. En francais, le ROS en est l'équivalent.
Merci à Werner - HB9AKN(sk) pour avoir attiré mon attention sur ce point.
 Répartiteur ou additionneur de puissance résistif
Répartiteur ou additionneur de puissance résistif
Question : Lors de l'examen de radioamateur on m'a posé la
question suivante que je ne comprend pas bien.
Un répartiteur HF (ou additionneur de puissance) est constitué comme suit.
Quelle est son impédance de fonctionnement?
Les réponses proposées sont :
50 ohms, 52 ohms, 55 ohms 60 ohms
Note : cette question n'est plus posée à l'examen.
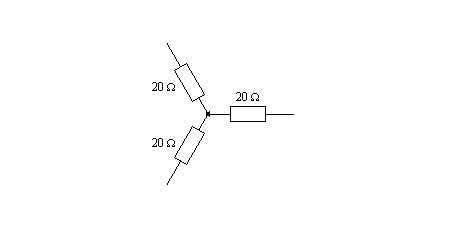
Je n'aime pas beaucoup cette question qui est pourtant simple quand elle est correctement posée. En effet, le schéma proposé n'est que trois résistances avec un point commun, difficilement un arrangement que l'on puisse qualifier de répartiteur HF ou d'additionneur de puissance. Il n'y a pas de connexion de masse, ni d'entrée, ni de sortie, ni rien, a part quelques mots passe-partout dans l'énoncé pour essayer de comprendre ce que l'on demande.
Voici donc le schéma correct et complet de ce que l'on demande. Soit un répartiteur ou un additionneur de puissance (plutôt d'une partie de la puissance comme nous le verrons plus bas). Quelle doit être l'impédance a ses bornes (Z) pour un fonctionnement optimal, c'est-a-dire pour que les sources et la charge soient correctement terminés. En fait quelle doit être l'impédance des sources et de la charge pour que tous les ports (port = entrée ou sortie) soient correctement chargés ?
Bien entendu, en raison des réponses multiples proposées, ce problème est posé à l'envers. Normalement, ce problème serait : soit 2 sources de 60 ohms et une charge de 60 ohms, comment les combiner avec trois résistances pour que les trois ports présentent la bonne impédance ?
Puisque nous avons la réponse dans l'énoncé (l'une juste, 3 fausses), on peut essayer chaque réponse jusqu'a ce que l'on tombe sur la bonne. La bonne sera celle qui donnera au troisième port la même impédance que celle appliquée aux deux premiers (OK. ce n'est pas très clair, voyons donc les exemples pratique).
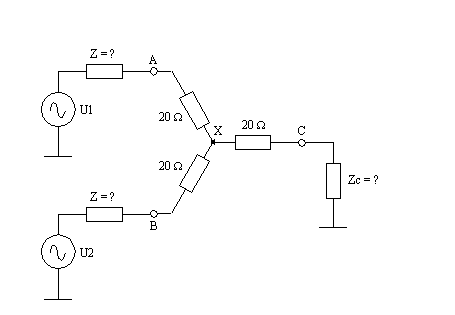
Soit Z(U1) = 50 ohms et Z(U2) = 50 ohms
Chacune de ces résistances est en série avec une résistance de 20 ohms pour un total de 70 ohms par branche. Mais comme il y a deux sources, au point X, les sources présentent 35 ohms (2 résistances de 70 ohms en parallèle).
Maintenant depuis le point X vers la charge il y a 20 ohms, qui en série avec les 35 ohms de notre (nos) source font 55 ohms. Ce n'est pas ce que nous voulons puisque les 3 ports doivent présenter la même impédance.
Essayons avec la seconde valeur proposée, soit 52 ohms. Maintenant les sources imposent au point X : 72 ohms/2 = 36 ohms. En série avec la troisième résistance de 20 ohms, cela donne 56 ohms. Toujours pas la bonne réponse.
Avec 55 ohms, le point X voit 37,5 ohms du coté des sources, ce qui impose 57,5 ohms du coté de la charge, ce qui ne fait toujours pas le compte.
Dernier essai avec 60 ohms. Les sources présentent 40 ohms au point X. En série avec les 20 ohms du port de la charge, cela donne 60 ohms.
C'est la bonne réponse. En fait si deux des ports sont chargés sur 60 ohms, l'impédance présentée sur le troisième est de 60 ohms aussi.
Rassurons-nous, à part comme question piège à l'examen, ce circuit a peu d'applications; en effet, essayons de voir quelle est la portion du signal de chaque source qui se retrouve dans la charge.
Considérons le schéma ci-dessous. Ici, seule une source est connectée et deux des ports sont terminés.
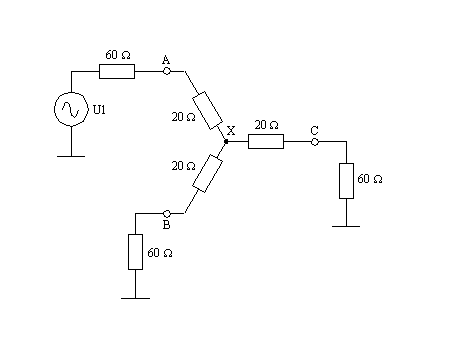
Voyons quelle est la puissance de la source disponible sur la charge. Dans le cas idéal (une source et une charge égales), la moitié de cette puissance est dissipée dans la charge et l'autre moitié perdue dans la source. Pour une source de 1 V dans 60 ohms (par exemple) la puissance totale fournie est de :
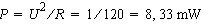
On utilise 120 ohms car la source et la charge ont les deux 60 ohms, ce qui signifie que la moitié de cette puissance est dissipée dans la source et seule l'autre moitié finit dans la charge, soit 4,16 mW.
Dans notre circuit, considérons la tension disponible dans la charge et ensuite calculons à quelle puissance cela correspond. En combinant les résistances en série, on obtient le schéma suivant :
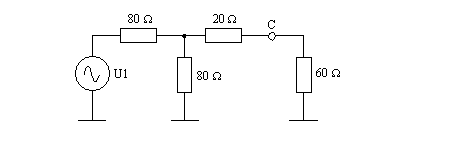
La combinaison de la résistance de 80 ohms verticale au centre et des résistances de 20 et 60 ohms vaut 40 ohms. La source voit donc 120 ohms. Ce courant provoque une tension aux bornes de la résistance de 80 ohms de la source et une tension aux bornes de la combinaison donnant 40 ohms proportionnellement à la valeur de ces résistances.
Une règle de trois nous permet de trouver la tension aux bornes de la combinaison de 40 ohms, soit 0,333 V. Cette tension est elle-même divisée dans la proportion de 20 et 40, selon les valeurs des deux dernières résistances du circuit, ce qui donne une tension de :
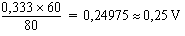
La puissance dans la charge est donc de :
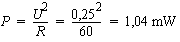
Ceci représente une puissance de -6 dB par rapport a celle que fournirait la source dans une simple charge de 60 ohms.
 Circuit DC avec 2 sources et 2 boucles
Circuit DC avec 2 sources et 2 boucles
Question : Je suis tombé sur la question suivante à l'examen, et je ne suis pas sûr
d'avoir répondu correctement. Quelle est la bonne réponse ?
Dans le circuit suivant, quel est le courant dans la résistance de 600 ohms ?
Note : cette question n'est plus au programme de l'examen depuis début 2007.
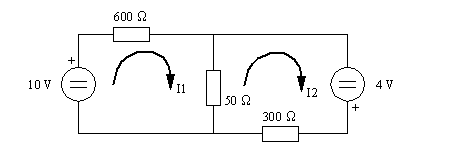
Il y a quatre manières de répondre à cette question. La première et la plus simple est de considérer les réponses offertes (que nous ne connaissons pas ici) et il y a fort à parier que seule l'une d'entre elles se situe aux alentour de 15 à 16 mA. En effet, le courant le plus important circulera dans la boucle externe (10 V, 600 ohms, 4 V, 300 ohms). Le courant dans la 50 ohms provenant de la source de 10 V (10 V/650 ohms=15,4 mA) étant plus ou moins annulé par celui en provenance de la source de 4 V (4 V/350 ohms=11,4 mA). Dans ces conditions, en première approximation, nous pouvons ne considérer que la boucle externe et prédire un courant de :
La seconde méthode est de calculer le vrai courant. Comme nous avons 2 boucles, nous devons écrire un système de 2 équations à 2 inconnues (I1 et I2). Soit I1 le courant dans la premiere boucle et I2 celui dans la seconde. Nous remarquons que I1 et I2 sont en opposition dans la résistance de 50 ohms. Les équations doivent décrire la somme des tensions le long de chaque boucle.
50.(I2–I1) + 300.I2 = 4 equ 2.
Regroupons les I1 et les I2.
–50.I1 + 350.I2 = 4 equ 4.
Il y a plusieurs méthodes pour résoudre ceci, utilisons la méthode dite de l'élimination (ici éliminons I2). Multiplions l'équation 3 par 7 (cela ne change en rien sa validité).
–50.I1 + 350.I2 = 4 equ 6.
Nous pouvons maintenant additionner les équations 5 et 6, ce qui va éliminer I2.
I1 est le courant qui traverse la résistance de 600 ohms. Cette valeur est assez proche de notre première estimation.
La troisième méthode est d'utiliser le théorème dit de superposition. Ce dernier permet de résoudre ce genre de problèmes en ne
considérant qu'une source à la fois. Les courants dans chaque résistance étant alors la somme des courants dûs à chaque source
séparément. La source qui est ignorée est remplacée par un court-circuit.
Les résistances de 300 ohms et de 50 ohms sont en parallèle, ce qui correspond à une résistance de 42,857 ohms.
La source de 10 V débite donc un courant dans une résistance équivalente de 642,857 ohms, ce qui donne 15,556 mA.Annulons maintenant la source de 10 V et considérons celle de 4 V. Cette dernière voit la combinaison de 600 et 50 ohms en parallèle, dite combinaison qui est en série avec la résistance de 300 ohms. Le courant dans cette boucle est de 11,556 mA. Il est maintenant aisé de calculer que la tension aux bornes de la résistance de 600 ohms est de 0,533 V. Cette tension donne lieu à un courant de 0,889 mA dans la résistance de 600 ohms. Ce courant s'ajoute donc à celui déjà calculé dans la résistance de 600 ohms, pour un total de :
Note Il est important de considérer le sens du courant dû à chaque source. Si par exemple la source de 4 V était dans l'autre sens (moins vers le haut), il aurait fallut soustraire le courant qui lui est dû du premier courant calculé pour trouver le courant total dans cette résistance.
Premièrement, enlevons la résistance qui nous intéresse, soit celle de 600 ohms. Considérons maintenant le circuit qu'il reste, et calculons la tension de Thèvenin qui est la tension présente aux bornes où la résistance de 600 ohms a été enlevée.
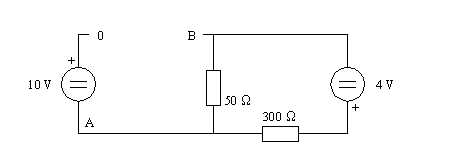
En partant du point 0 il y a la source de 10 V jusqu'au point A puis la tension dans la résistance de 50 ohms jusqu'au point B . La tension dans la résistance de 50 ohms est aisée à calculer puisque seule la source de 4 V y contribue.
La tension totale aux bornes de la résistance temporairement supprimée est donc de 10,57145 V. Ceci est la tension dite de Thèvenin.
Il nous reste mainteanat à trouver la résistance de Thèvenin.
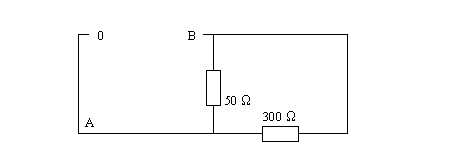
Cette dernière est la résistance vue des bornes ou se trouvait la résistance de 600 ohms, mais avec toutes les sources de tension remplacées par un court-circuit. Ici il s'agit simplement de la combinaison en parallèle des 2 résistances restantes, soit une résistance de 42,857 ohms.
Finalement, le schéma équivalent selon Thévenin est le suivant, dans lequel nous avons rebranché la résistance de 600 ohms::
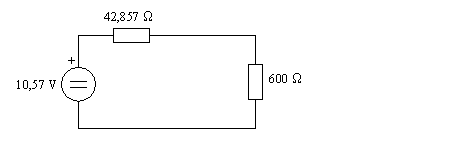
Calculons le courant dans la boucle, qui est celui dans la résistance de 600 ohms, et donc la réponse demandée:
Question : J'avais appris que le Q d'un circuit RLC est donné par Q = xl/R , or il semble que cette formule ne marche pas dans tous les cas, qu'en est-il ?
Considérons les différentes topologies de circuits RLC. Les deux principales sont le circuit série, aussi appelé circuit réjecteur et le circuit parallèle, aussi connu sous le nom de circuit bouchon.
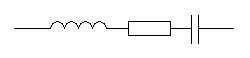 | 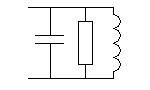 |
| Circuit RLC série | Circuit RLC Parallèle |
Afin d'éviter des maths, pas parlants pour tout le monde, tentons une approche intuitive.
Circuit Série :
Dans un circuit série, le courant est nécessairement le même dans les 3 éléments montés en série, par contre la tension est en avance de
90° dans la bobine et en retard de 90° dans le condensateur.
A la résonnance, ces deux tensions sont égales (puisque xL = xC) mais en opposition, puisque 2 fois 90° valent 180°
ce que l'on décrit souvent en plaçant un signe – devant xC. Ces deux tensions partielles s'annulent donc, et toute la tension
aux bornes du circuit se retrouve aux bornes de la résistance.
Le Q d'un circuit est une mesure (inverse) des pertes dans ce circuit, or des pertes ne peuvent se produire que dans la résistance (des éléments purement réactifs ne sont le siège d'aucune puissance réelle). Puisque la puissance dissipée dans une résistance vaut : R · I2 , on voit que plus la résistance sera faible, moins les pertes seront importantes et plus le Q du circuit sera élevé. C'est exactement ce que nous indique la formule pour le Q d'un circuit série :
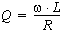
On voit bien ici que plus R est faible, plus Q est élevé (Q est inversement proportionnel à R).
Voici quelques autres formules sur le Q d'un circuit série :
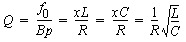
En pratique, un circuit série présente une impédance faible à sa fréquence de résonnance est une impédance élevée aux autres fréquences, ce qui est une fonction utile en électronique. Par contre avec R élevée, ce circuit présenterait une impédance élevée à toutes les fréquences, ce que l'on peut effectuer avec une simple résistance ; L et C n'ont alors quasiment plus d'effet.
Circuit Parallèle :
Dans un circuit parallèle, la tension est nécessairement le même dans les 3 éléments montés en parallèle, par contre le courant est en avance de
90° dans le condensateur et en retard de 90° dans la bobine.
A la résonnance, ces deux courants sont égaux (puisque xL = xC) mais en opposition, puisque 2 fois 90° valent 180°
ce que l'on décrit souvent en plaçant un signe – devant xC. Ces deux courants partiels s'annulent donc, et le seul courant
débité par la source passe dans la résistance.
Le Q d'un circuit est une mesure (inverse) des pertes dans ce circuit, or des pertes ne peuvent se produire que dans la résistance (des éléments purement réactifs ne sont le siège d'aucune puissance réelle). Puisque la puissance dissipée dans une résistance vaut : U2/R , on voit que plus la résistance sera importante, plus les pertes seront faibles et plus le Q du circuit sera élevé. C'est exactement ce que nous indique la formule pour le Q d'un circuit parallèle :
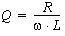
On voit bien ici que plus R est élevé, plus Q est élevé (Q est proportionnel à R).
Voici quelques autres formules sur le Q d'un circuit parallèle :
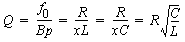
En pratique, un circuit parallèle présente une impédance élevée à sa fréquence de résonnance, et une impédance faibles aux autres fréquences, ce qui a bien des applications en électronique, par contre avec R faible, L et C seraient court-circuités, et donc sans effet.
Circuit « hybride » :
On peut aussi envisager un circuit tel celui ci-dessous :
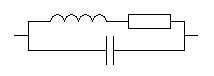 |
| Circuit RLC « hybride » |
Ce circuit est bien évidemment un circuit parallèle, je l'ai appelé « hybride » ici pour les besoins
de la cause. Notons au passage que la résistance dans ce circuit et ainsi que dans les deux ci-dessus ne représente pas forcément un
élément discret (c'est-à-dire séparé), elle représente généralement l'ensemble des pertes dans le circuit (résistance du
fil de la bobine, effet pelliculaire, pertes dans l'isolant du condensateur, pour ne citer que les principales).
Dans ce circuit on pourrait admettre que l'on ne considère que les pertes en rapport avec la bobine, ce qui est souvent
justifié, puisque ce sont les plus importantes.
Avant d'appliquer l'une au l'autre des formules ci-dessus, observons ce circuit en gardant à l'esprit les notions discutées plus haut.
Avec R élevée, la bobine est quasiment mise hors circuit, il est peu probable que ce soit correct. Cependant, avec R faible, ce circuit prend la forme classique d'un circuit parallèle RL. Poussons la réflexion un peu plus loin pour nous assurer que la formule à utiliser ici est bien celle applicable aux circuits série.
Quand nous avons mentionné ci-dessus que dans un circuit parallèle, les courants dans la bobine et le condensateurs s'annulaient, il eut été plus exact de mentionner qu'un courant circule sans pertes entre le condensateur et la bobine. Tour à tour, le courant circulant dans la bobine, charge le condensateur jusqu'à une certaine tension, puis le condensateur se décharge dans la bobine, y donnant lieu à un courant, et ainsi de suite.
La résistance dans le circuit ci-dessus est ainsi parcourue par le même courant que celui au travers des éléments L et C dans le circuit série, et va causer des pertes par le même mécanisme. Il faut donc ici appliquer la même formule que pour le circuit série.
Note : ce circuit n'est pas au programme de l'examen de radioamateur, mais a été présenté ici pour attirer l'attention du lecteur sur l'importance de ne pas appliquer des formules sans bien comprendre d'abord le problème à résoudre.
 Distance et puissance d'un émetteur
Distance et puissance d'un émetteur
Question : Un récepteur reçoit deux émetteurs A et B. A est distant de 50 km et fait
1 kW. B distant de 85 km est reçu avec la même intensité.
Quelle est sa puissance ? Quelle formule utiliser ?
PE 3.20, du livre Le RADIOAMATEUR, Manuel de
Référence
En effet le cours ne donne pas directement une formule pour répondre à cette question, mais le texte précise :
La puissance d'un signal s'atténue d'une façon proportionnelle au carré de la distance (Il y a une erreur dans cette phrase dans la troisième édition du livre, voir l'Errata) - erreur corrigée dans les éditions suivantes. Cela signifie que si, à une certaine distance d'un émetteur, on reçoit un signal avec une certaine puissance, au double de la distance, le signal sera reçu avec une puissance quatre fois plus faible. En ce qui concerne la tension à l'antenne de réception, elle s'atténue de façon proportionnelle à la distance (Section 25.2.2).
Commençons par représenter ce que nous donne l'énoncé par un dessin.
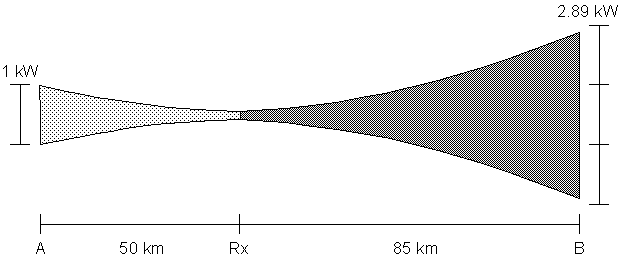
A gauche, au point A, la puissance est de 1 kW, et s'atténue en fonction du carré de la distance jusqu'au récepteur (Rx). A droite, au point B, la puissance est de 2,89 kW, et s'atténue en fonction du carré de la distance jusqu'au récepteur (Rx). La puissance reçue par le récepteur est la même dans les 2 cas.
Notons en passant que s'il s'était agit de tensions, l'atténuation (en tension) serait directement proportionnelle à la distance puisque :
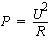 (La puissance varie au carré de la tension.)
(La puissance varie au carré de la tension.)
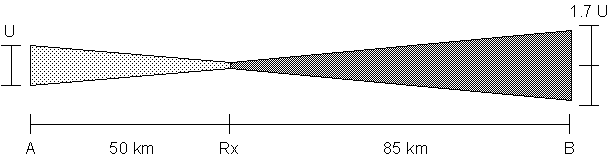
Méthode 1 :
Le rapport des distances est de : 85/50 = 1,7Puisque l'atténuation en puissance est proportionnelle au carré de la distance, la puissance requise au point B est de :
1.72 = 2,89 fois plus importante, soit 2,89 kW.Méthode 2 :
Nous pouvons aussi utiliser une règle de trois, en tenant compte du fait que nous nous intéressons au carré des distances :PB = 1 . 852/502 = 2,89 kW
Méthode 3 :Nous pouvons aussi considérer les tensions, mais c'est une solution plus longue. Bien entendu nous ne connaissons pas la résistance en jeu ici puisque :
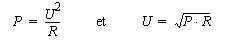
mais puisque nous effectuons des comparaisons de puissances, cette résistance est la même dans tout le système. Nous pouvons donc choisir une valeur appropriée pour les calculs, soit pas exemple 50 ohms ou même 1 ohm, c'est cette valeur que nous utiliserons ici.
Tension sur l'émetteur A :
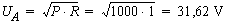
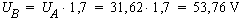
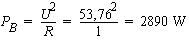
 Coefficient de température et ppms
Coefficient de température et ppms
Question : J'ai une résistance de type PT100 dont le coefficient de température est donné à 3850ppm/K. Qu'est ce que cela signifie et comment s'en servir ? Ma résistance est censée faire 100 Ω à 0°C, et je mesure 108,5 Ω à 22°C.
Une PT100 est une résistance de mesure de température, qui fait 100 Ω à 0°C et qui augmente de résistance avec la température.
Un coefficient de température (ici d'une résistance en fonction de la température, mais ce pourrait aussi être par exemple la variation de fréquence d'un quartz en fonction de la température) permet de calculer la variation de la valeur de cet élément en fonction de la température. Ce coefficient représente la variation pour un changement de température de 1 degré (Celsius ou Kelvin) d'une unité de l'élément concerné. Une unité de résistance est 1 Ω, et pour un quartz ce serait 1 Hz. Un coefficient de température peut être exprimé en pourcents (%), pour mille (‰) ou part par million (ppm). 0,01 = 1% = 10‰ = 10'000ppm Comme on peut le voir, le pourcent est une une valeur plutôt importante, c'est pourquoi, pour des petites variations, on lui préfère le ppm. 1ppm = 0,001‰ = 0,0001% = 0,000'001 Notons encore que ces valeurs peuvent s'écrire :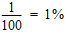

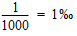

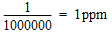 Considérons une résistance de 1 Ω (à 20°C par exemple) ayant un coefficient de +200ppm. Quelle sera sa valeur à 21°C (soit une variation de 1°C) ?
Cette résistance vaudra 1 Ω plus une petite variation de 200ppm par degré. Ici le changement de température vaut 1 degré, et la résistance vaudra :
1 + 0,000'200 = 1,000'200 Ω
Cette même résistance vaudrait pour une variation de 30°C :
1 + 30 × 0,000'200 = 1,006 Ω
Une résistance de 1000 Ω à 20°C ayant le même coefficient de température vaudrait à 50°C :
1000 + 1000 × 30 × 0,000'200 = 1000 × (1 + 30 × 0,000'200) = 1006 Ω
Le premier 1000 représente la valeur de la résistance à froid.
Le second 1000 est nécessaire puisque le coefficient de température est donné pour une valeur unitaire de la résistance, soit 1 Ω.
Le 30 est nécessaire puisque la variation de température est de 30°C.
Finalement le coefficient de température pourrait tout aussi bien s'écrire :
Considérons une résistance de 1 Ω (à 20°C par exemple) ayant un coefficient de +200ppm. Quelle sera sa valeur à 21°C (soit une variation de 1°C) ?
Cette résistance vaudra 1 Ω plus une petite variation de 200ppm par degré. Ici le changement de température vaut 1 degré, et la résistance vaudra :
1 + 0,000'200 = 1,000'200 Ω
Cette même résistance vaudrait pour une variation de 30°C :
1 + 30 × 0,000'200 = 1,006 Ω
Une résistance de 1000 Ω à 20°C ayant le même coefficient de température vaudrait à 50°C :
1000 + 1000 × 30 × 0,000'200 = 1000 × (1 + 30 × 0,000'200) = 1006 Ω
Le premier 1000 représente la valeur de la résistance à froid.
Le second 1000 est nécessaire puisque le coefficient de température est donné pour une valeur unitaire de la résistance, soit 1 Ω.
Le 30 est nécessaire puisque la variation de température est de 30°C.
Finalement le coefficient de température pourrait tout aussi bien s'écrire :
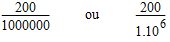 Venons-en finalement à notre PT100. Sa valeur est de 100 Ω à 0°C. La variation de température est de 22°C, et son coefficient de température est de 3850ppm/K. On peut donc écrire :
100 + 100 × 22 × 3850/1E6 = 100 × (1 + 22 × 3850/1E6) = 108,47 Ω
Ce dernier calcul n'est autre que la formule standard pour calculer la valeur d'une résistance en température :
Venons-en finalement à notre PT100. Sa valeur est de 100 Ω à 0°C. La variation de température est de 22°C, et son coefficient de température est de 3850ppm/K. On peut donc écrire :
100 + 100 × 22 × 3850/1E6 = 100 × (1 + 22 × 3850/1E6) = 108,47 Ω
Ce dernier calcul n'est autre que la formule standard pour calculer la valeur d'une résistance en température :
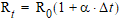 Note : les degrés Celsius et Kelvin sont identique sauf pour leur valeur de départ. Les degrés Celsius commencent à 0°C et les degrés Kelvin commencent à -273°C. Donc 0°C correspondent à 273°K, et 22°C correspondent à 295°K. Cependant une variation de 1°C est égale à une variation de 1°K.
Note : les degrés Celsius et Kelvin sont identique sauf pour leur valeur de départ. Les degrés Celsius commencent à 0°C et les degrés Kelvin commencent à -273°C. Donc 0°C correspondent à 273°K, et 22°C correspondent à 295°K. Cependant une variation de 1°C est égale à une variation de 1°K.
 Question 8.1 (maintenant 9.1) du fascicule de l'OFCOM, puissance PEP et tension efficace
Question 8.1 (maintenant 9.1) du fascicule de l'OFCOM, puissance PEP et tension efficace
Question : J'ai quelques difficultés avec votre réponse dans le « Guide d'étude » pour la question 8.1 du fascicule de l'OFCOM, en particulier avec les tensions de crête et les tensions efficaces :
L'OFCOM ne publie plus ce document. Voici quel était l'énoncé de cette question : On mesure 100 W pour la puissance de la porteuse d'un émetteur AM (A3E). On mesure également 100 W avec un wattmètre PEP. Si l'émetteur est maintenant modulé à 100% par un signal audio, quelle puissance indiquera le wattmètre PEP ?
Quelle que soit la tension sinusoïdale considérée, la tension efficace est toujours égale à 0,707 fois la tension de crête. Si l'on considère la figure C) ci-dessous, on voit à gauche que pour la partie HF non modulée, la tension efficace [HF Ueff] est 0,707 x la tension de crête [HF Upk]. De même, à droite, pour le cycle de plus grande amplitude, la tension efficace [Ueff max] vaut 0,707 fois la tension de crête [Upk max]. Ces valeurs sont reportées sur ce graphe en pointillé épais.
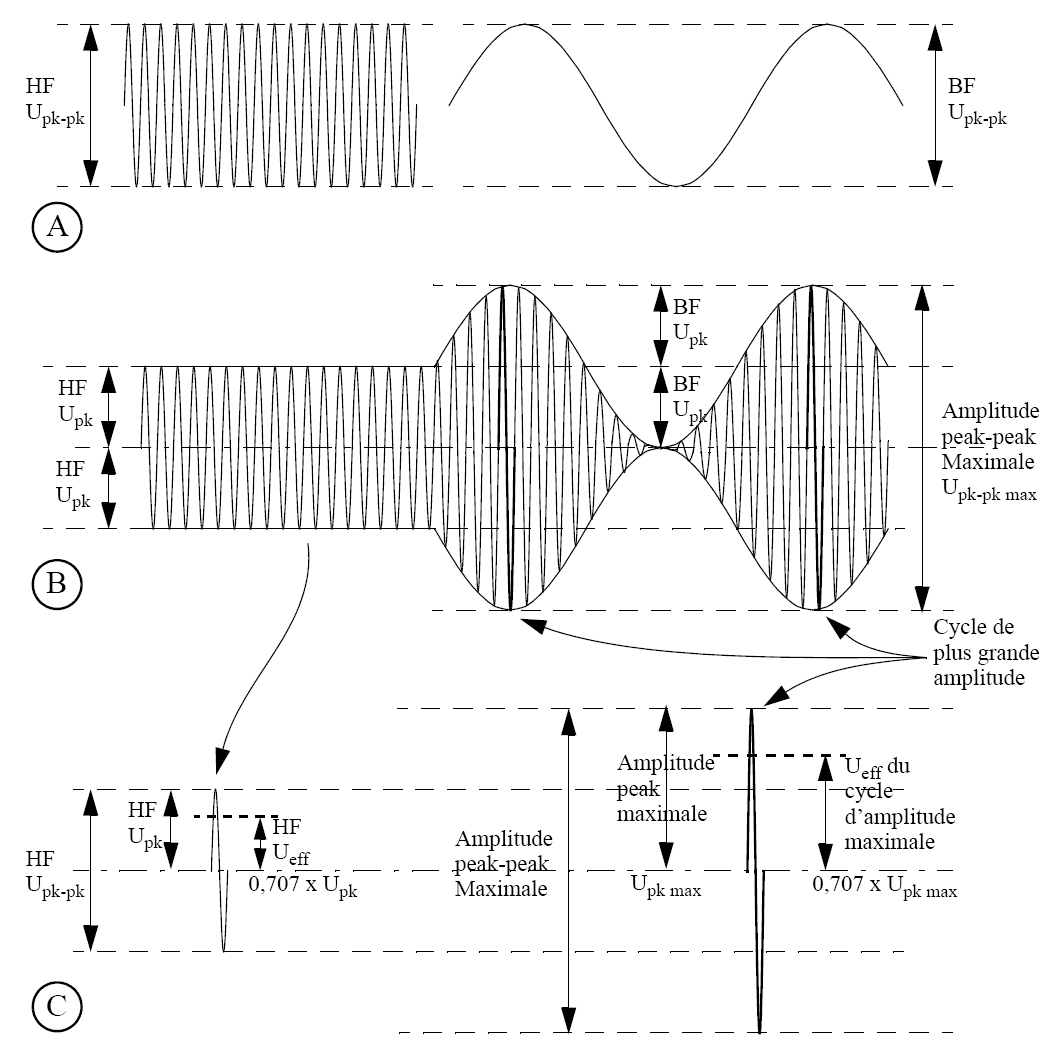
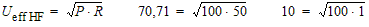 La tension efficace au cycle de plus grande amplitude vaut 2 fois cette valeur :
La tension efficace au cycle de plus grande amplitude vaut 2 fois cette valeur :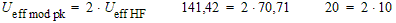 Finalement la puissance PEP peut être calculée :
Finalement la puissance PEP peut être calculée :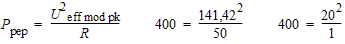 En conclusion, la figure ci-dessous met en évidence les valeurs que nous venons de calculer
En conclusion, la figure ci-dessous met en évidence les valeurs que nous venons de calculer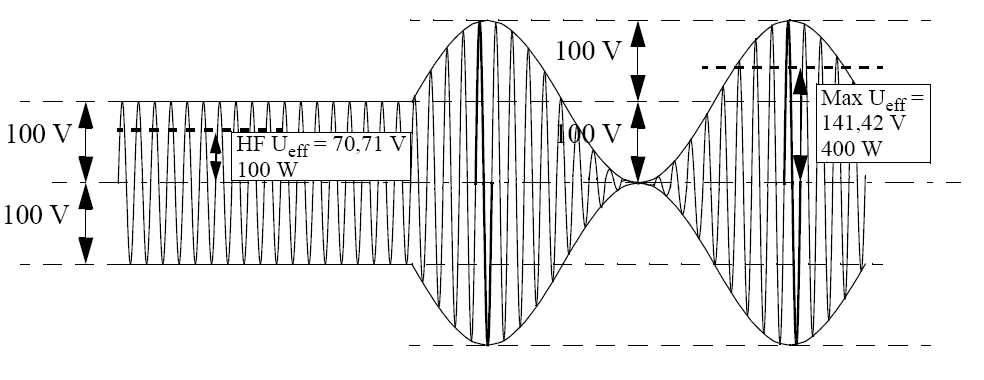
 Décibels de tension et décibels de puissance
Décibels de tension et décibels de puissance
Question : J'ai quelques questions concernant les dB (décibels). En effet, on parle de dB de puissance qui ne seraient pas les mêmes que les dB de tension, j'ai même entendu parler de faux dB quand on compare des tensions sur des impédances différentes, par exemple sur un filtre RC. Qu'en est-il ?
La réponse est simple, il n'y a qu'une sorte de dB, et les faux dB n'existent pas.
Premièrement voyons le cas des dB de tension qui ne seraient pas les mêmes que les dB de puissance.
Considérons un amplificateur d'impédances d'entrée et de sortie de 50 ohms. On mesure 1 V sur son entrée et la puissance à l'entrée peut être calculée ainsi :
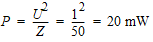
La tension en sortie est mesurée à : 3,162 V
Calculons encore la puissance de sortie :
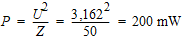
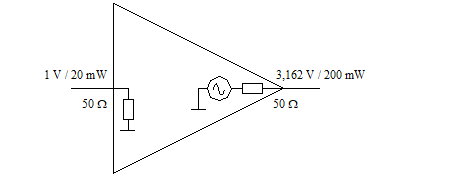
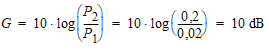
Puisque les impédances sont identiques en entrée et sortie, effectuons le même calcul au moyen des tensions :
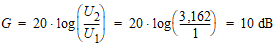
Une tension au carré est équivalente à une puissance. Le fait de prendre 20 · log(x) est égal à 10 · log(x2) ; en cas de doute, essayer ces 2 calculs sur votre calculette.
Donc dans les 2 cas ci-dessus, nous avons calculé un rapport de puissances. Les décibels servent à représenter des rapports de puissances.
Considérons maintenant un amplificateur d'impédances d'entrée de 150 ohms et de 50 ohms de sortie. On mesure 1,732 V à l'entrée et 3,162 V en sortie.
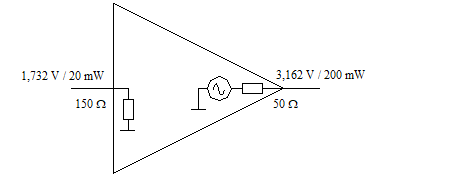
On ne peut évidemment pas calculer le gain au moyen des tensions puisque les impédances ne sont pas identiques. Il nous faut donc le calculer au moyen des puissances.
Puissance d'entrée :
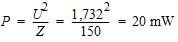
Puissance de sortie :
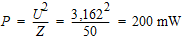
Le gain dans ce cas est de :
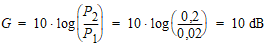
A ce stade il est aisé de conclure qu'il n'y a qu'une sorte de dB et qu'ils sont utilisés uniquement pour mesurer des rapports de puissances.
Voyons maintenant le cas du filtre RC passe bas :
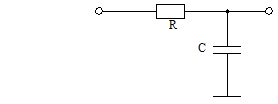
Il est évident que l'impédance du condensateur dépend de la fréquence, et donc que les impédances d'entrée et de sortie ne sont pas constantes. Cependant ici, on ne s'intéresse pas à la puissance, mais plutôt aux tensions en entrée et en sortie. Dans ce cas, on néglige les impédances pour se concentrer sur les tensions seulement. Ceci est d'autant plus justifié que la sortie du filtre ira vers l'entrée à haute impédance de l'étage suivant, et qui dit haute impédance, implique tension mais quasiment pas de courant, donc quasiment pas de puissance.
Ainsi, pour un filtre RC, à la fréquence de coupure, pour disons 1 V en entrée, on a 0,707 V en sortie. Ceci est la définition de la fréquence de coupure du filtre.
Nous pouvons calculer le rapport en dB de ces 2 tensions, pour trouver :
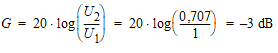
Posons-nous quelques questions sur ce résultat :
Est-ce que ce résultat est juste ? Oui, car c'est exactement ce que nous attendons de la fréquence de coupure d'un filtre passe-bas.
Est-ce que cela correspond à la définition formelle du dB ? Non, car on ne tiens pas compte des impédances.
Pouvons nous utiliser ce résultat ? Oui, parce que dans ce cas, les impédances sont tout à fait secondaires et nous nous concentrons sur le rapport des tensions.
Est-ce que cette façon de faire est universellement acceptée et utilisée ? Oui et oui.
Exemple : prenons le cas d'un émetteur, nous nous intéressons à sa puissance dans les étages finaux, mais tout au long du traitement interne des signaux, il est plus utile de considérer des tensions, les puissances en jeu étant faibles.
Conclusion : Les dB servent à comparer 2 puissances dans la plupart des cas, cependant, quand les puissances en jeu sont faibles et que l'on se concentre sur des différences de tensions, il est accepté (et d'usage courant) de déroger à la définition formelle des dB, et de comparer des tensions sans se soucier des impédances, qui dans ce cas seront généralement élevées et donc pas le siège d'une puissance appréciable.
 Question 4.17 (maintenant 5.17) du fascicule de l'OFCOM, filtre notch
Question 4.17 (maintenant 5.17) du fascicule de l'OFCOM, filtre notch
L'OFCOM ne publie plus ce document. Voici quelle était cette question :
Question : Pour le problème 4.17 proposé par l'OFCOM dans leur recueil de questions d'examen, ils donnent D) comme bonne réponse et vous n'êtes pas d'accord avec cette réponse concernant le rôle d'un filtre notch. Pouvez-vous expliquer votre point de vue.
La question posée par l'OFCOM est :

La réponse qui vient immédiatement à l'esprit, avant même d'avoir vu celles proposées, est : un filtre destiné à atténuer une fréquence indésirable.
En effet, si vous êtes à votre station et qu'un sifflement gênant vous dérange, vous aller enclencher le filtre notch pour l'éliminer, vous n'allez pas enclencher le notch pour éliminer « toutes les fréquences dans une petite plage de fréquences ».
Si l'on vous demande de concevoir un filtre notch pour éliminer, par exemple, du 50 Hz, vous allez travailler sur un filtre notch pour éliminer du 50 Hz. Dans cette spécification, il n'y a qu'une seule fréquence (ici, 50 Hz).
Il est vrai qu'en réalité, une fois votre filtre réalisé, il va présenter une certaine largeur de bande (à -3 dB) et donc plus ou moins atténuer un groupe de fréquences autour de la fréquence centrale, ici 50 Hz. Il n'en demeure pas moins que ce filtre a été conçu pour atténuer 50 Hz.
D'ailleurs dans un autre problème l'OFCOM se contredit et semble d'accord avec moi : problème 7.31 qui dit « On construit un circuit réjecteur (notch) au moyen d'une section de câble coaxial (coefficient de vitesse 0.8) pour 145.000MHz. » et non pas un filtre notch pour éliminer les fréquences de 144,950 MHz à 145,050MHz par exemple.
Si maintenant nous désirons concevoir un filtre pour atténuer les fréquences entre disons 45 et 55 Hz, nous allons devoir faire un effort pour avoir une atténuation plus ou moins constante entre 45 et 55 Hz, nous sommes ici en présence d'un filtre coupe-bande (et donc pas d'un notch). Ici nous avons une fréquence de coupure basse (45 Hz) et une fréquence de coupure haute (55 Hz) il s'agit donc ici d'un filtre réjecteur de bande.
Considérons maintenant un autre aspect de notre démarche pour devenir radioamateur. Nous avons précisé que nous appliquions un principe de première approximation (nous considérons les éléments étudiés comme parfaits) sauf s'il est précisé autrement. Or dans cette question il n'est justement pas précisé que nous considérons un filtre réel.
Finalement considérons le sens du mot « pour », selon le dictionnaire Larousse. Ce mot peut avoir plusieurs sens, mais celui qui nous intéresse est : Le but. Synonymes : afin de - dans le but de - en vue de.
Donc les réponses proposées par l'OFCOM sont :
C) Un filtre dans le but d'atténuer une seule fréquence de perturbation.
D) Un filtre dans le but d'atténuer toutes les fréquences dans une petite plage de fréquences.
Au vu de ce qui précède, la réponses C) correspond à la définition du notch, on désire atténuer une fréquence perturbatrice et ce faisant on atténue aussi quelques fréquences de part et d'autre de notre fréquence centrale car rien n'est parfait.
Quand à la réponse D) elle correspond clairement à la définition d'un filtre coupe-bande où l'on définit on « plage » de fréquences à atténuer.
Poussons quand même plus loin nos considérations. Si l'on s'intéresse maintenant au comportement des éléments étudiés en réalité - en ignorant notre principe de première approximation, sans le préciser - alors nous allons devoir considérer que :
- Un filtre passe-bande BF ayant une bande passante de 300 à 3000 Hz devra être considéré comme laissant passer des fréquences de 100 à 3500 Hz (je vous laisse juge de la « marge » à ajouter).
- Toutes nos sources de tension ont une résistance interne - et il faudra souvent en tenir compte.
- Toutes nos résistances auront une tolérance et nos résultats ne seront qu'approximatifs, sans mentionner qu'elles introduisent du bruit dont il faudra parfois tenir compte.
- Puisque toutes les bobines ont une résistance interne, elle n'introduiront plus un déphasage de 90°, de même pour les condensateurs.
- Nos transistors n'ont plus un β constant, ce dernier dépendant du courant de collecteur, et la valeur de β donnée dans l'énoncé d'un problème n'est plus qu'une valeur indicative d'un ordre de grandeur.
- Nos transformateurs n'auront plus un rendement de 100%, et il faudra en tenir compte.
- Nos diodes silicium n'auront plus un Uf de 0,6 V, Uf dépendra du courant dans la diode, cela compliquera quelquefois nos calculs.
- etc...
Soyons donc sérieux et conséquents, utilisons autant que possible notre principe de première approximation, et considérons les éléments et circuits étudiés comme parfaits sauf s'il est précisé autrement :
Un filtre notch est destiné à atténuer une fréquence mais en réalité affecte aussi les fréquences de part et d'autre de cette dernière en fonction de son Q.
Un filtre réjecteur de bande est destiné à atténuer une bande de fréquences (petite ou pas), mais en réalité affecte aussi les fréquences de part et d'autre de ses fréquences de coupure.
Donc la réponse à la question « Qu'est ce qu'un filtre réjecteur (notch filter) » est :
- Un filtre destiné à atténuer une seule fréquence de perturbation.
et la réponse à la question : Qu'est ce qu'un filtre réjecteur de bande est :
- Un filtre destiné à atténuer toutes les fréquences dans une (petite) plage de fréquences.
Dernière remarque : si vous pensez que j'ai tord d'être aussi rigoureux, n'oubliez pas que c'est peut-être à cause du (ou des) point que vous obtiendrez ou pas en réponse à cette question que vous passerez ou échouerez à votre examen. D'ailleurs il m'arrive de m'interroger sur le pourquoi de ces questions peu précises et de ces réponses approximatives, voire fausses. Serait-ce pour qu'il ne soit pas possible de passer cet examen avec 100% ce qui indiquerait qu'il est trop facile...
 Symboles courants et symboles obscurs
Symboles courants et symboles obscurs
Question : (2024) Je viens de passer l'examen HB3 de radioamateur et j'ai eu une question sur un symbole de résistance accompagné d'une sorte de lettre ressemblant à v manuscrit que je ne connaissait pas. Que pouvez-vous en dire ?
Après quelques recherches j'ai trouvé la question originale avec le symbole mentionné.
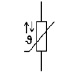
Il existe une grande variété de résistances spéciales, soit d'un usage courant, soit d'un usage moins courant. De même, il existe des symboles spécifiques pour la plupart de ces résistances, certains évidents et clairs, certains moins clairs et d'autres particulièrement obscurs. De plus ces symboles varient enter les USA (dont les symboles sont les plus courants) et les Européens, dont les symboles sont surtout utilisés en Allemagne selon mes observations, sans compter que les Allemands utilisent aussi une norme qui leur est propre (DIN : Deutsches Institut für Normung). De plus certains organismes et entreprises créent leurs propres symboles qui devienent eux aussi populaires, mais souvent ce ne sont que des variations des symboles les plus « standards ». Typiquement les symboles US sont les plus utilisés en raison de leur création qui prédate les symboles EU, mais aussi car, les Américains étant pragmatiques, ils ont l'avantage d'être clair et simples. Les symboles EU sont en général moins évidents à interprêter, et c'est peut-être la raison de leur acceptation limitée, sauf apparemment par les pays germanophones. Bien entendu ces remarques ne concernent pas seulement les symboles pour les résistances, mais aussi les symboles pour les fonctions logiques et les ampli-ops par exemple. Remarquablement les symboles pour les transistors (de toutes sortes) sont (quasiment) identiques dans les deux systèmes. Le tableau ci-dessous résume les symboles d'un usage courant en électronique, mais aussi ceux rarement utilisés, mais que l'OFCOM se plait d'utiliser pour corser l'examen. Une derniére remarque avant de passer à un tableau récapitulatif, en Suisse, nos autorités compétentes fédérales sont germanophones, ce qui a pour conséquence qu'à l'examen nous rencontrerons les symboles EU. Cependant pour brouiller les cartes encore plus, certains des symboles utilisés appartiennent à la norme DIN (Deutsches Institut für Normung) utilisés uniquement en Allemagne mais donc aussi à Bienne.
|
Composant |
US |
EU |
DIN |
Commentaire |
|---|---|---|---|---|
|
Ajustable |

|

|

|
|
|
Variable linéaire |

|

|

|
|
|
Variable non linéaire |

|

|

|
|
|
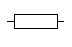
Résistance |
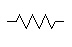
|
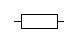
|
|
DIN : Le corps de la résistance est un peu plus long. |
|
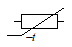
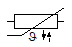
NTC |
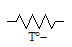
|
|
|
Negative Temperature Coefficient : Résistance à coefficient de température négatif. La valeur de la résistance diminue quand la température augmente. Les petites flèches sur le symbole DIN, indique que l'une augmente quand l'autre baisse. Quant à la lettre grecque, il s'agit d'une version manuscrite, rare et peu connue de la lettre theta ϑ, utilisée ici pour représenter la température. |
|
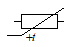
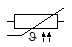
PTC |
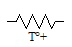
|
|
|
Positive Temperature Coefficient : Résistance à coefficient de température positif. La valeur de la résistance augmente quand la température augmente. Les petites flèches sur le symbole DIN, indique que l'une augmente quand l'autre augmente. Quant à la lettre grecque, il s'agit d'une version manuscrite, rare et peu connue de la lettre theta ϑ, utilisée ici pour représenter la température. |
|
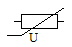
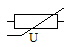
VDR ou varistor |
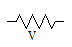
|
|
|
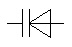
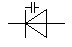
Voltage dependant resistor : La valeur de la résistance dépend de la tension à ses bornes. Typiquement la résistance diminue quand la tension dépasse un certain seuil. |
|
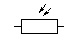
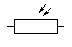
LDR |
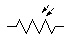
|
|
|
Voltage dependant resistor : La valeur de la résistance diminue en présence de lumière. |
|
Potentiomètre |
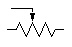
|
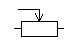
|
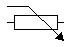
|
EU : La flèche peut être pleine |
|
Bobine |
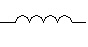
|

|
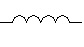
|
Le symbole EU est rarement utilisé. |
|
Condensateur |
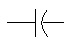
|
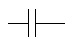
|
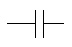
|
|
|
Condensateur électrolytique |
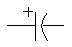
|
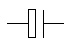
|
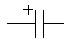
|
Le symbole EU est rarement utilisé. |
|
Diode Zener |
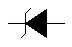
|
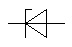
|
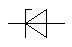
|
|
|
Diode varicap ou varactor |
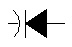
|
|
|
|
|
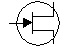
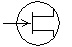
JFET |
|
|
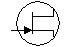
|
EU : La flèche peut être aussi en face de la source. |
 Calcul de la largeur de bande d'un signal en FSK
Calcul de la largeur de bande d'un signal en FSK
Question : Dans votre livre, la formule pour le calcul de la largeur de bande d'un signal en FSK est BFSK = 1,2 · shift + Bd or il me semble qu'une formule dérivée de la règle de Carson serait plus appropriée, qu'en est-il ?
Le calcul de la largeur de bande d'un signal en FSK est abordé et traité de multiples façons suivant les auteurs. Nombre de questions ne sont pas considérées dans ces traitements qui souvent ne regardent que la théorie pure sans considérations pour le finalité de cette transmission.
Certains des aspects à considérer sont :
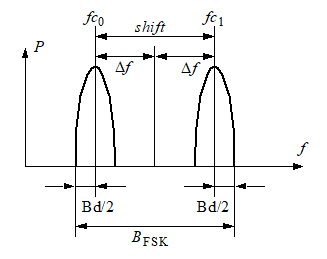
La déviation totale (shift) est la distance ente les deux tons (fc0 et fc1). Cette déviation se divise en 2 Δf. La largeur des pics dépend directement de la vitesse de transmission (Baudrate).
Plusieurs formules sont publiées pour le calcul de la largeur de bande :
Voici un tableau comparatif pour trois des types de FSK utilisés par les radioamateurs.
|
Source |
Carson |
DARC |
UIT/ARRL |
Autres |
|---|---|---|---|---|
|
Formule |
BFSK = 2(Δf + Bd) |
BFSK = 2(Δf + 1,6 · Bd) |
BFSK = 1,2 · shift + Bd |
BFSK = 2Δf + Bd |
|
Vitesse = 45,45 Bd ; shift = 170 Hz |
261 Hz |
315 Hz |
250 Hz |
216 Hz |
|
Vitesse = 1200 Bd ; shift = 1000 Hz |
3400 Hz |
4840 Hz |
2400 Hz |
2200 Hz |
|
Vitesse = 9600 Bd ; shift = 4800 Hz |
24000 Hz |
33600 Hz |
15360 Hz |
14400 Hz |
Dans le cas de la vitesse de 45,45 Bd et du shift de 170 Hz, on s'attend à une largeur de bande de l'ordre de 250 à 260 Hz.
Dans le cas de la vitesse = 1200 Bd et du shift = 1000 Hz, on s'attend à une largeur de bande de l'ordre de 2500 à 3000 Hz.
Dans le cas de la vitesse = 9600 Bd et du shift = 4800 Hz, on s'attend à une largeur de bande de l'ordre de 15 à 20 kHz.

|

|

|